Exactly three times as many? Do you count all surfaces that form triangles or only the white ones?
If I understand where this us going, the additional triangles will all be of the small white variety to hit the target of 3x triangle increase. If we consider negative space triangles and composite triangles, the next phase of the fractal will probably have more than 3x the triangles but that math is hard and I don’t have a notebook
Current shape x3, start with triangle > Triforce > Triforce of Triforces and so on
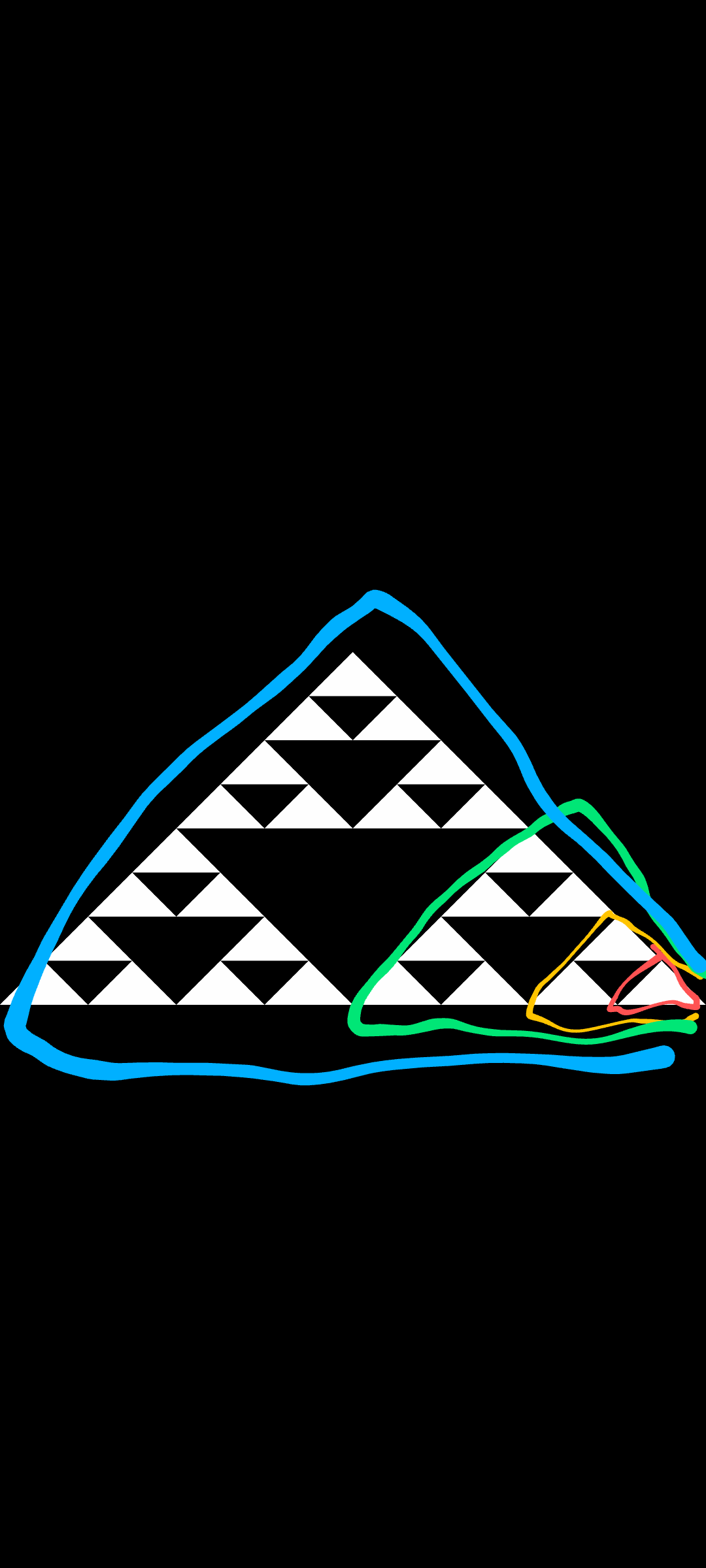
Looking at the image from here in my bed, it looks like with each iteration, you get 3x as many white triangles, and 3x+1 as many black triangles between white triangles as there were before. At iteration 1, you have 1 white triangle and 0 black triangles.
I’m too lazy to double check.
You can’t keep getting away with this! Is there no end to this madness?!
Oh, great. It’s the Wind Waker Triforce shards all over again.
Better start collecting charts…
How can I stay updated in this saga? Voyager cant sub me to your user, or add notifications to this sub…
there’s a new entry in the saga: https://lemmy.world/post/19799395
I count
3342 triangles, counting black space and outlines made of other triangles.40…
Each Triforce is 4 triangles, each Triforce of Triforces adds an extra triangle in the middle ((3x4) +1) so that’s 13 and then the next step is 3x that + the extra triangle in the middle = 40
Without the black spaces it’s 27
They said counting outlines made of other triangles too. So each triforce is 4 triangles. The whole is itself a triangle. Which makes it 3x + 2, for a total at third level of 44.
I was only counting "by color"but if we add the outline as well then a Triforce is 5 triangles (three white,1 black, the shape itself), the Triforce of Triforces is 3 x 5 + 2 (middle + outline) so 17 and the shape as it is now is 3 x 17 + 2 so 53
Yup, i also counted black ones and also got 53
Same but without all the fancy words. 53.
Shit I was tired, but I meant 42, counting the top right and left black areas too.
MORE!
When you break the triforce into smaller, more digestible pieces
That takes Courage.
Into to programming PTSD trigger
All possible formulas for the amount of triangles are as follows.
Let A(n) be the total number white of triangles in the n’th run.
Let B(n) be the total number of triangles in the n’th run in the structure that does not include the two corner triangles.
Let C(n) be the total numbers of triangles in the n’th run including the corner triangles.
Then we the following starting numbers and recursive formulas hold:
A(1)=1 and A(n+1)=3A(n) for all integers n>0
Reason: previous structure is embedded exactly 3 times
B(1)=1 and B(n+1)=3B(n) + 2 for all integers n>0
Reason: previous structure is embedded 3 times and this creates 1 new center triangle and 1 new greater triangle
C(1)=3 and C(n+1)=3(C(n) - 2) + 4 for all integers n>0
Reason: previous structure with the corner triangles removed is embedded 3 times, similar to previous case, and we add the 2 corner triangles at the end.
For this run (n=4) that means A(4)=27 B(4)=53 C(3)=55
For the fifth iteration!







